三角形重心坐标公式的诞生(从一个三角形重心性质的证明谈起)
三角形重心有一个性质,即从重心到顶点的距离是到对边距离的两倍。请看人教版教材八年级下册第62页第16题。题目呈现:
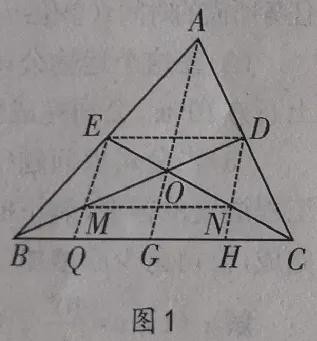
如图一,在△ABC中,D、E是边AC,AB上的中点,BD与CE相交于点O,BO与OD的长度有什么关系?BC边上的中线是否一定过点O?为什么?
我们知道本题的结论是:BO=2OD,BC边上的中线一定过点O。教材以课后习题的形式告诉我们一个结论:三角形的三条中线交于一点(重心),并且这一点到顶点的距离是到对边中点距离的两倍。
要证明这一个关于三角形重心的性质,是常见的证明线段有两倍关系的题目。我们用平面几何方法和解析几何方法分别给出证明。解析法还可得到一个副产品:
三角形重心坐标公式。
平面几何
我们考虑利用平行四边形的性质来给出证明。
解 分别取BO和CO的中点M和N,顺次连接MN,ND,DE,EM. ∵DE是△ABC的中位线∴DE∥=½BC.(打不出来平行等于的符号,用两个符号代替,下同),又∵点M和点N分别是BO和CO的中点∴MN是△OBC的中位线∴MN∥=½BC∴DE∥=MN.四边形MNDE是平行四边形∴OM=OD,OE=ON.又∵BM=OM,CN=ON,∴BO=2OD,CD=2OE.
第一小问证明完毕。现在考虑怎么证明第二小问。
证明三角形的三条中线交于一点,容易想到两种思路,一是由两条中线交于一点,再证明另外一条中线也通过这个交点;二是证明两两中线的交点是重合的。除此之外,还可以考虑用面积法给出证明。根据以上思路,我们给出三种证法。
证法一:如图二,设BD,CE交于点O,连接ED,AO,并延长AO交BC于点G,交ED于点K。由于DE∥BC,并且BO=2OD,CO=2OE,根据平行线分线段成比例的定理可得:
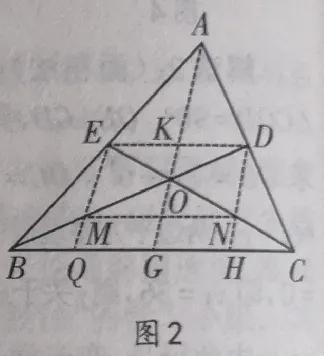
DK:BG=DO:OB=1:2,DK:CG=AD:AC=1:2,∴BG=CG,∴点G是BC的中点∴AG是△ABC的中线∴△ABC的三条中线交于一点。
证法二:如图三,
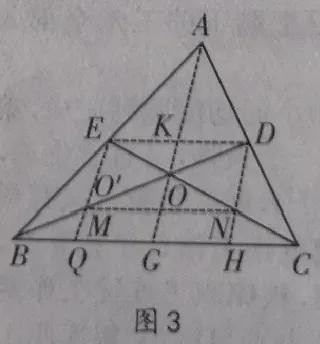
设BD和CE交于点O,由于BO=2OD,设中线BD和AG交于点O',由于BO'=2O'D,即O'是BD的三等分点之一,由三等分点的唯一性可知,点O和点O'重合,即三角形的三条中线交于一点。
证法三:(面积法)如图四,
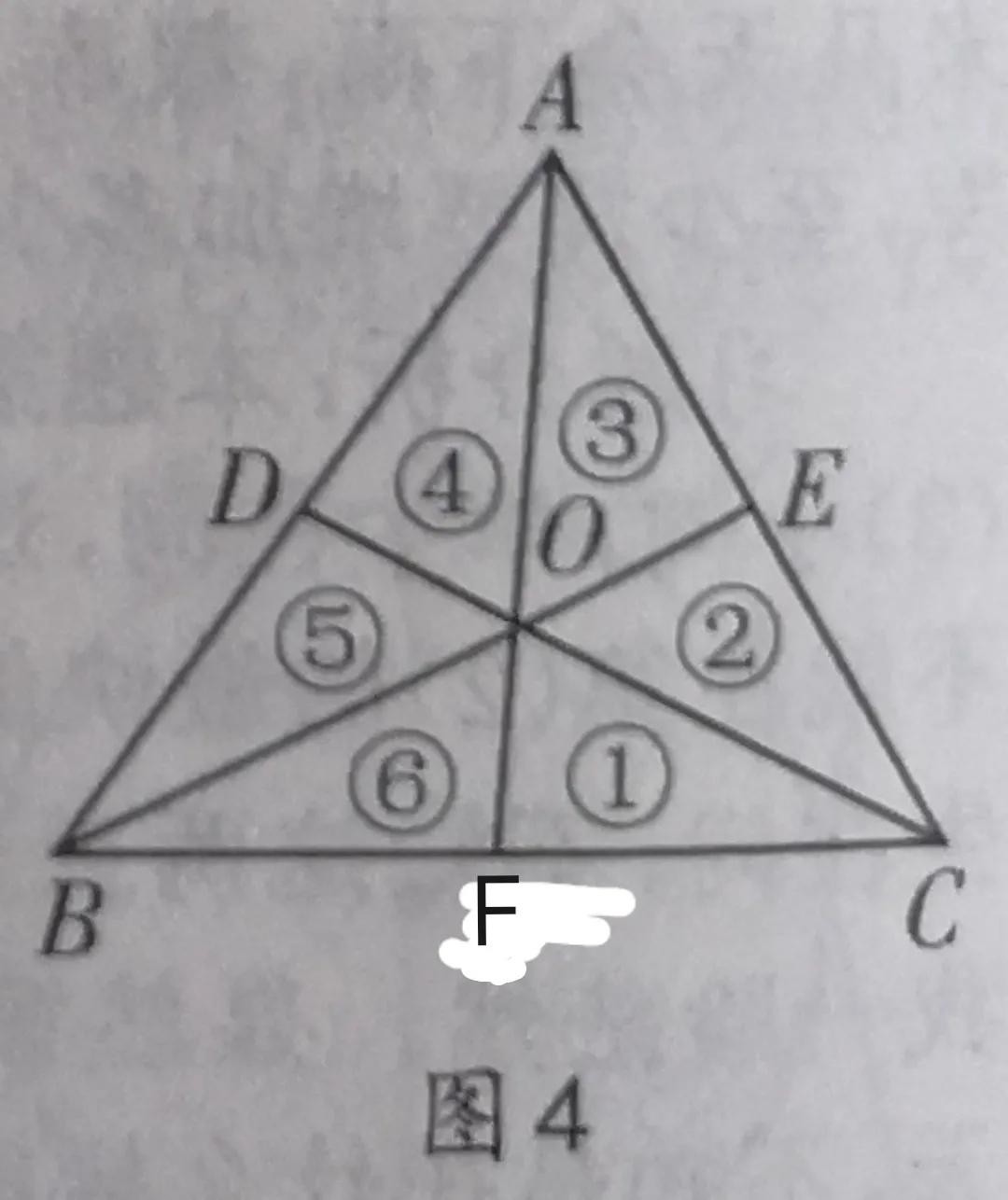
设△ABC的两条中线BE和CD交于点O,连接AO并延长交BC于点F。这三条线把△ABC的面积分成6个小三角形,如图标注所示。这些小三角形的面积用标注的序号表示。∵BE是△ABC的中线∴点E是边AC的中点,∴②=③,同理可证④=⑤又∵点D,E是边AB和AC的中点∴①+②+⑥=½S△ᴀʙᴄ,
①+⑥+⑤=½S△ᴀʙᴄ; ∴②=⑤
∴②=③=④=⑤.
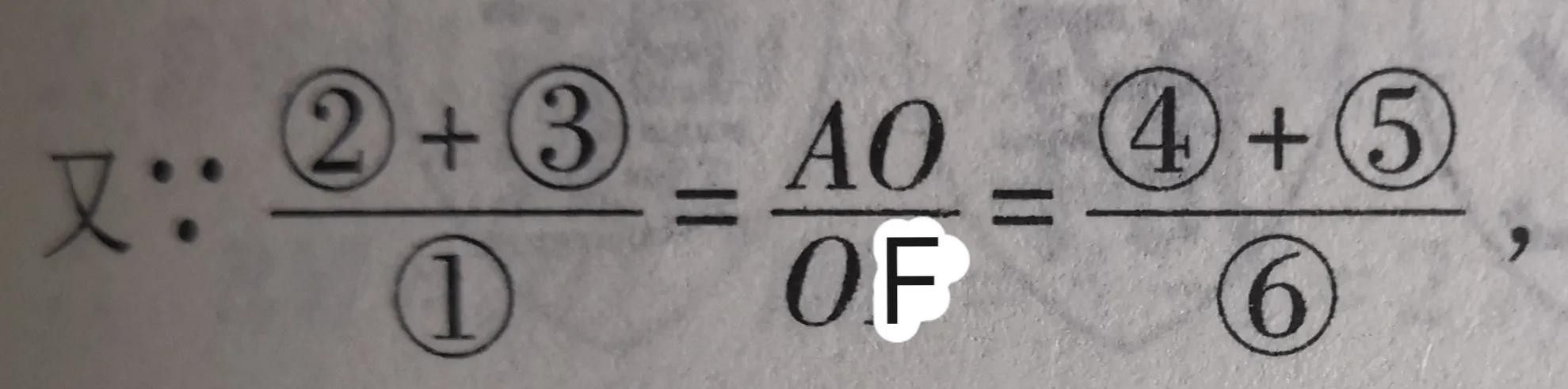
∴①=⑥∴BF=CF,∴点F是BC的中点所以三条中线AF,CD,BE交于点O。也就是说三角形的三条中线把三角形分为6个等面积的小三角形。由此可得三角形重心的另外一个性质:三角形的重心与三个顶点的连线把三角形分成三个等面积的三角形。
以上内容引自《中小学数学》2022年1~2月中旬(初中版),作者袁宏老师。
现在我们的压轴戏要登场了。
解析几何
题目呈现:试证三角形的三条中线交于一点,此点在每条中线上离顶点三分之二处。
解题思路:可任意选择两条中线,各求它的三分之二分点(顶点为起点),假如它们的坐标相同,就是两点合一,说明两条中线交于一个定点。同样可以证明第三条中线也经过这一点。这样就命题得证。证明步骤如下:
建系是必须的
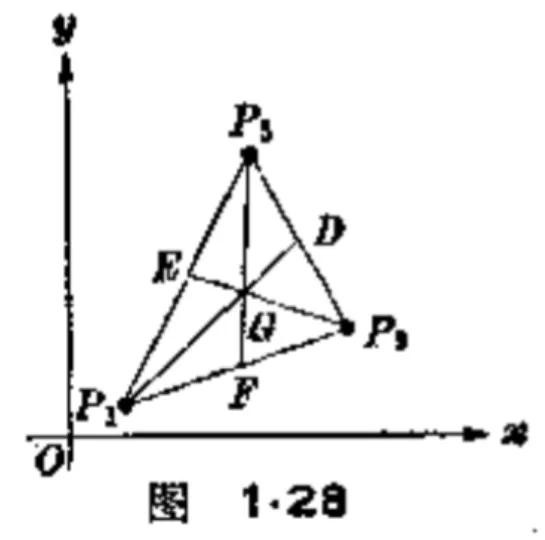
设三角形的三个顶点为P₁(x₁,y₁),P₂(x₂,y₂),P₃(x₃,y₃),中线为P₁D,P₂E,P₃F。即D,E,F分别为各边的中点(如图1.28)它们的坐标是
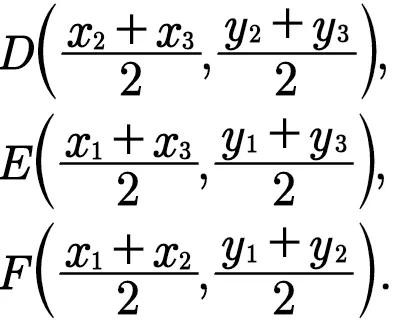
又设中线P₁D,P₂E上各有一点G,G',且
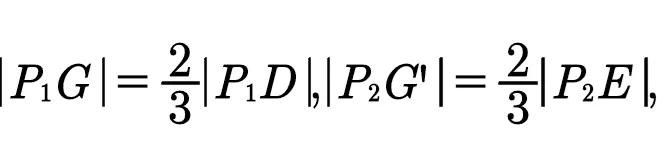
即|P₁G|=2|GD|,|P₂G'|=2|G'E|,
G在P₁和D两点之间,故λ=2.设它的坐标是(x,y),则
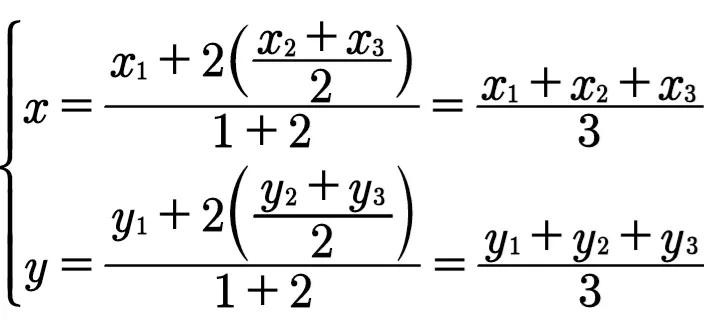
G'在P₂和E两点之间,故λ'=2.设它的坐标是(x',y'),则
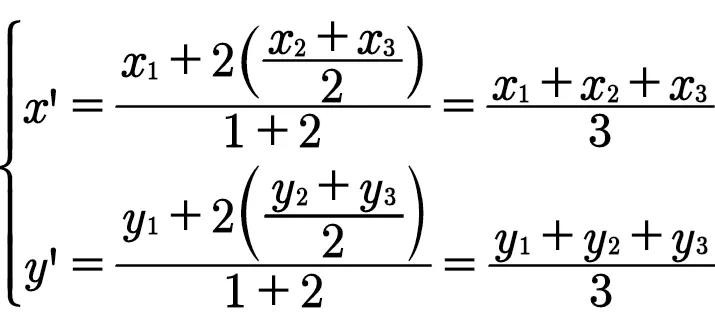
所以x=x',y=y',就是说G和G'两点合一,也就是中线P₁D,P₂E相交于一个定点。同样,如P₃F上有一点G'',而
|P₃G"|=2/3|P₃F|,即|P₃G"|=2|G"F|.可证点G"的坐标也是
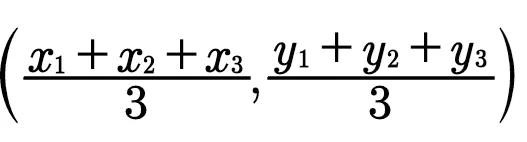
也合于G点。所以一个三角形的三条中线交于一点,此点与三个顶点的距离各在相应中线的三分之二处。G点称为三角形P₁P₂P₃的重心,三角形重心坐标公式为
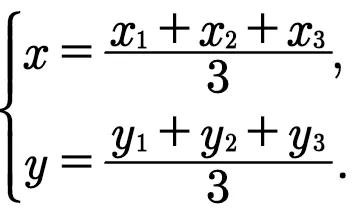
三角形重心坐标公式的诞生
本节内容引自《平面解析几何》(数理化自学丛书第二版)。
以上证明用到了一个知识的点:线段的定比分点坐标公式:(即公式1)
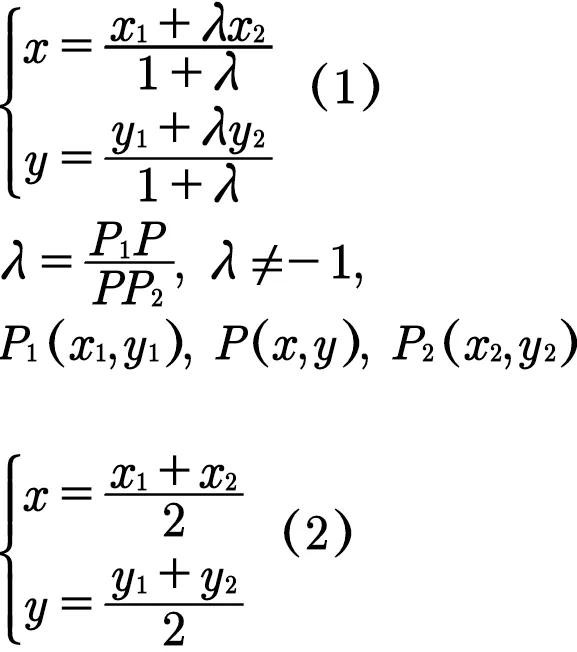
当λ=1时,就是定比分点坐标公式的特例——中点坐标公式。(即公式2)
科学尚未普及,媒体还需努力。感谢阅读,再见。




