初高衔接:平方平均数与统计,算术平均数与平方平均数
初高衔接:平方平均数与统计,算术平均数与平方平均数
初高衔接:毕达哥拉斯与调和平均数
初高衔接:射影定理和几何平均数
初高衔接:几何视角下的基本不等式:算术平均数和几何平均数
笔者已经分别介绍了三种平均数,接下来是最后一种平均数:平方平均数
一、平方平均数
![]()
平方平均数(quadratic mean),又名均方根(Root Mean Square),是指一组数据的平方的平均数的算术平方根。
如果用
![]()
来表示数据,那么
![]()
二、平方平均数的数学应用
很遗憾,笔者并没有在高中数学中找到平方平均数的具体应用
不过,我们可以借助这个理解方差以及标准差
根据初中所学,
![]()
我们发现,如果将方差开方就会得到
![]()
我们如果将
![]()
那么实际上这就是
![]()
的平方平均数
我们把
![]()
记作
![]()
,称为这组数据的标准差,读作sigma,就是
![]()
的小写
即
![]()
至于为什么要开根号搞出这么一个东西呢?
我们先回顾一下方差的作用:方差是用来衡量数据同平均值的偏离程度,方差越大,数据的离散程度就越大
实际上如果原始数据的单位为
![]()
,那么方差的单位就是
![]()
,单位不同,方差并不能直接让我们感知到数据是怎么离散的,因为平方的关系,方差可能远远大于原始数据.
但是标准差是方差的平方根,换而言之,标准差的单位和原始数据是一样的!
标准差本质上也是一种平均数!是数据相对平均数距离
![]()
的平方平均数!
所以标准差就可以理解为数据相对于平均数的平均距离!
这个我们会在高三的正态分布中见识到它的威力,不过这里我们暂且搁置一笔
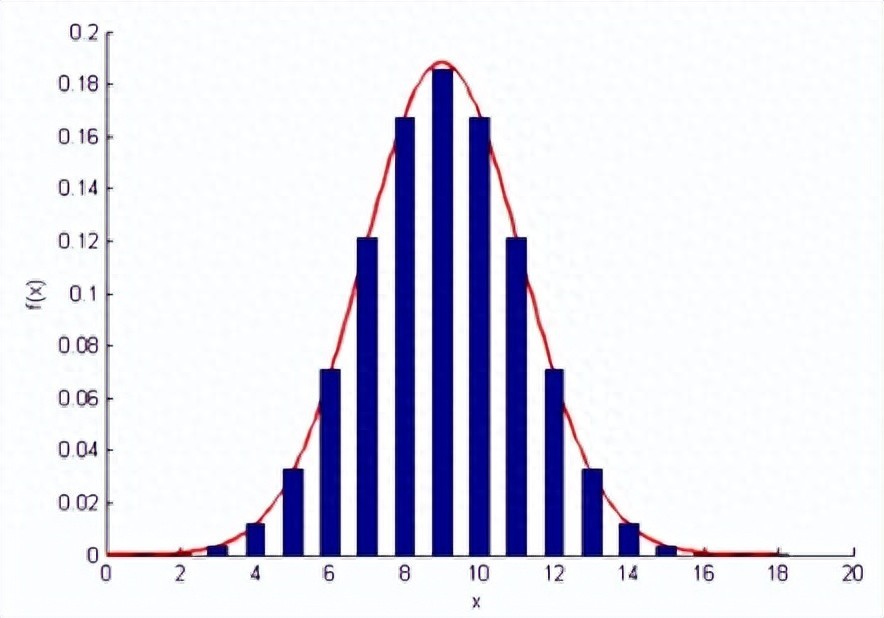
正态分布图像
三、平方平均数在高中物理中的应用
我们简要提一下匀加速直线中的物理公式
![]()
![]()
我们经常关心的是,物体在运动过程中的速度
比如
![]()
那么运动员在50m的速度快还是在5s的时候速度快呢?
![]()
![]()
得
![]()
那么五秒时的速度,
![]()
而50m的速度则是,
![]()
,得
![]()
显然,中间位移的速度更大!这也是符合常识的,启程一半的时间肯定是大于后一半的时间,到位移中点时,时间早已过去一半!
也就是说位移中点速度大于中间时刻速度
下面我们给出数学证明
假设初始速度为
![]()
,最终速度为
![]()
位移中点可以用两个式子求解
![]()
![]()
右边相等,那么
![]()
那么
![]()
而时间中点就是平均速度,
![]()
等等!如果我们换个字母呢?
就是比较
![]()
和
![]()
换而言之,就是算数平均数和平方平均数的比较!
四、算数平均数和平方平均数
根据均值不等式
![]()
高中阶段,我们只需要明白n=2的情况
下面我们将证明
![]()
这里要用到分析法,可以参考初高衔接:基本不等式的基本运用
只需证
![]()
只需证
![]()
也就是
![]()
整理得
![]()
,显然成立,因此证明完毕
因此我们得到了十分重要的结论:
算数平均数小于等于平方平均数
它的物理意义是中间时刻速度小于中间位移速度!
望读者有所收获
标签:

137
从受欺凌的少年到残忍的杀人魔:泰德·邦迪的一生 泰德·邦迪是美国历史上最臭名昭著的连环杀手之一。他于1970年代末至1980年代初在美国多个州杀害了至少30名年轻女性,并被认为有...

92
穿越文三部曲,一本更比一本香!男主极尽风流女主国色天香 各位书友晚上好,今天小洁给大家分享几部好高评分的现穿越小说,喜欢的书友们记得点赞收藏! 第一部《妃常穿越:千...

114
2019胡润百富榜发布 马云第三次成中国首富!完整胡润百富榜榜单一览附全文内 容 2019胡润百富榜新鲜出炉了!相信大家都非常好奇2019胡润百富榜上榜富豪有哪些,他们都分布在什么行...

178
强推-闲听落花经典文集锦 墨桑 作者:闲听落花 角色: 顾晞/李桑柔/顾瑾 进度:完成 简介 锦桐 作者:闲听落花 进度:完成 简介 盛华 作者:闲听落花 进度:完成 简介: 玉堂金闺 作者:闲...

145
女性尖锐湿疣的早期症状图片 大家都知道尖锐湿疣有很严重的危害,如果不及时治疗还会引发并发症。但是大部分患者都不能够得到及时的治疗,原因是不了解尖锐湿疣有哪些临床症状...

125
看赵薇大学时期的照片,一双大眼非常迷人 赵薇当年凭借《还珠格格》中的小燕子一炮而红,可以说是红遍了大江南北,也让赵薇顺利的走向了娱乐圈的一线女星行列。 上面的照片是...

56
黄艺:曾经被称为“王哲林的接班人”,要将自己的天赋兑现。 #挑战30天在头条写日记# 黄艺 1999年 207cm 95kg 漳州漳浦,效力于福建队 福建青年队出来的球员,曾经被称为“王哲林的接...

141
猴魁多少钱一斤? 猴魁茶,一种营养元素十分高的荼叶,内含有咖啡因、茶氨酸、碳水化合物等化学物质,拥有抑菌、提升精气神、消除疲劳、可改进血液循环系统、活血化淤等作用,...

83
何为意难平? 意难平最初的意思是:心中有一股情绪难以平静下来。 现在逐渐演变成一个网络流行语,代指的是心中不能释怀、放不下的事情或者是人,由此产生一种不甘心的感觉。...

193
高质量古言好文书单,唯独深情不忍辜负,除却真心无以为报 《尚书大人,打发点咯》 《佳偶》 《一城春弄》 《国色生香》 《掌柜攻略》 《旧时乌衣》 《陛下有个黑月光》 《虞家...

100
凤凰之力到底多恐怖? 可能看过X战警的小伙伴都知道“凤凰女”很厉害,但是又不太明白凤凰之力到底强在何处?它究竟是一种什么样的力量?以及它到底起源于何处?又如何遗传的...

198
「关注」敦化至白河高铁开工,4年后游长白山更方便了! 日前,国家“十三五”规划中,沈阳到佳木斯高速铁路的重要组成部分——吉林敦化到白河高速铁路正式开工建设。 敦化至白...

189
《奇迹再现》带来的童年回忆杀 我们都是光,《迪迦奥特曼》中《奇迹再现》这首歌,成就了毛华锋,也是他人生反转开始的起点,也是多少少年,年少时的回忆! 2004年2月,《迪迦奥...

135
“小哥”费玉清再出新段子,这样的费玉清你肯定没见过! 不了解费玉清的人,都认为小哥的职业是歌手,多了解一点的人都知道其实小哥是个很有喜感的段子手,“你追我,你要是追...

116
余男:演艺传奇中的人生新篇 余男,这位中国内地影坛的杰出女演员,1976年9月5日诞生于辽宁大连这片美丽的土地,毕业于北京电影学院表演系。她的演艺生涯如同一幅绚丽多彩的画卷...

159
西野加奈 图片来源于网络 图片来源于网络 西野加奈(Nishino Kana)是日本著名的女歌手和词曲创作人,出生于1989年3月18日。她于2008年以单曲《I》正式出道,并迅速在日本乐坛崭露头角...

85
双十一剁手表情包微信,双11专用表情包搞笑图片 一年一度的双十一又又又来了,你的钱包准备好了吗?是不是马上就要连土都吃不起了,为大家整理了一些表情包,喜欢的抱走吧~...

168
年味不散,民俗盛宴,带你感受潍坊北海民俗祭海节 2月6日,农历正月十六,第七届潍坊北海民俗祭海节在潍坊滨海旅游度假区举行。当地渔民、盐民群众以及来自北京、济南等地的游...

137
就在今天!库科奇保持了29年的纪录被打破了 库科奇是公牛第二个三连冠时期的重要成员,来自欧洲的他被誉为欧洲乔丹、巴尔干魔术师,他在国际篮球比赛中的表现非常出色,比如...

156
旧羽绒服改造羽绒被 6月份网购羽绒被被壳,想把不穿的旧羽绒服改成羽绒被,也算是废物利用。由于各种原因,当然也有懒的因素,迟迟未付诸行动。最近突然又有断舍离的心思,看...







































